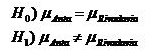
Identificamos los siguientes puntos que los alumnos necesitan repasar y aclarar:
A propósito del problema del posible efecto de la aplicación de diferentes dosis de compost sobre la concentración de N del suelo, revisamos los siguientes términos:
Continuando con el problema, recordamos el significado del coeficiente de determinación R² y dijimos que podemos considerarlo una mediada de cuán asociada está la variable respuesta a los efectos.
Luego nos concentramos en recordar que R² es el cociente de suma de cuadrados de la regresión sobre la suma de cuadrados totales. Planteamos las fórmulas de las sumas de cuadrados totales, de la regresión y del error y mostramos los desvíos que se suman en cada una de ellas sobre un gráfico de dispersión. Finalmente recordamos que la suma de cuadrados totales es igual a la suma de cuadrados de la regresión más la suma de cuadrados del error.
SCTot = SCReg + SCErr
Esta suma se llama análisis de la varianza.
En este punto recordamos que para estimar la varianza de los errores usamos al cuadrado medio del error
CMErr = SCRrr / (n-2)
dónde n-2 es el valor de los grados de libertad del error. Entonces presentamos una alternativa al estadístico R², el cociente del cuadrado medio de la regresión sobre el cuadrado medio del error y dijimos que volveríamos a discutir esto hacia el final de la clase.
Planteamos el caso de un funcionario provincial que necesita comparar el contenido promedio de Arsénico en el agua de los pozos de los departamentos de Anta y Rivadavia (Salta). Discutimos el muestreo, las hipótesis y la prueba en la forma en que hicimos en el curso de Estadística General.
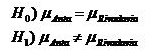
Luego propusimos que el contenido de Arsénico esperado (promedio) en el agua de un pozo del dto. de Anta puede ser expresado como la suma del contenido promedio en los pozos de ambos departamentos más un efecto Anta y que, del mismo modo, el contenido de Arsénico esperado en el agua de un pozo del dto. de Rivadavia ser expresado como la suma del contenido promedio en los pozos de ambos departamentos más un efecto Rivadavia.
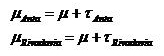
De este modo, se pueden plantear las mismas hipótesis en términos de los efectos
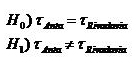
Sobre esta base planteamos el problema de la comparación entre contenidos esperados de Arsénico en forma de un modelo parecido al de regresión.
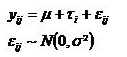
Sobre este modelo señalamos la variable respuesta, los efectos de los tratamientos y el error experimental.
A continuación discutimos la importancia de estas tres condiciones en el diseño experimental:
En relación con la repetición propusimos que (a) permite verificar si las diferencias observadas en la respuesta están asociadas con efectos de los tratamientos o no, y (b) permite aumentar la precisión de las estimaciones de valor esperado de la respuesta dado un tratamiento o de las diferencias entre los efectos de los tratamientos. Esto último se relaciona con el teorema central del límite que vimos en estadística general y relacionamos con implicancias de este tipo.
En relación con la aleatorización y con la independencia, propusimos que es necesaria para poder comparar los efectos efectivamene planteados en el modelo y no otros.
En relación con el control de la heterogeneidad, recordamos que el experimento de sorgo visto en el campo tenía bloques y comentamos cómo esto puede permitir aumentar la potencia de la prueba estadística. Aclaramos que volveríamos sobe esto en un par de semanas.
Volvimos a concentrar la atención sobre la comparación entre Anta y Rivadavia para hacer notar que, cuando el análisis incluye sólo dos tratamientos, el problema se puede resolver con las herramientas adquiridas en estadística general (prueba de t). En cambio, cuando interesa comparar más que dos tratamientos la prueba de t no sirve y es necesario contar con una alternativa. esta alternativa es la prueba de F basada en el análisis de la varianza.
Mediante un gráfico de dispersión visualizamos cómo esperaríamos que fuesen los cuadrados medios de los tratamientos y del error en el caso en que los tratamientos no tienen efectos diferentes y en el caso en que si tienen efectos diferentes. A partir de la idea intuitiva desarrollada de este modo volvimos a plantear la fórmula del estadístico F y mostramos que tendería a tomar valores altos cuando los tratamientos tienen efectos diferentes.
Con esto dimos la consigna de estudiar los capítulos 2 y 3 (Análisis de la Varianza y Modelo lineal) y prepararse para discutir en clase la solución del problema 5.
Comenzamos revisando la cuestión planteada por el problema 5 discutido en la clase práctica de esta semana. En este problema se presenta un experimento en el cual se comparan los efectos de diferentes momentos de aplicación de un fertilizante nitrogenado (y de un tratamiento testigo sin fertilizante) sobre el contenido de nitrógeno de los granos de cebada. Antes de examinar el modelo estadístico nos detuvimos a aclarar un poco el MODELO CONCEPTUAL en el que se basa este estudio. Este modelo conceptual incluye el conocimiento de las diferentes etapas del desarrollo de las plantas de cebada y de aspectos clave de la dinámica del nitrógeno en el suelo. Las ideas qe presentamos justifican la pregunta central que motiva el experimento (p.ej. en diferentes momentos de su desarrollo las plantas de cebada no tienen la misma capacidad para absorber el nitrógeno aplicado como fertilizante) y permiten identificar variables relevantes que convendría medir y analizar. La estadística contribuye a este proceso de generación de conocimiento con pautas para obtener datos representativos y con métodos para producir resúmenes apropiados de dichos datos y para evaluar en crédito que merecen los resultados.
Para ilustrar las pautas para la obtención de información representativa, propusimos un ejemplo apropiado para comprender que la asignación aleatoria de los tratamientos (momentos de fertilización) a las unidades experimentales es indispensable para poder atribuir los efectos observados a dichos tratamientos.
A continuación:
 ,
,
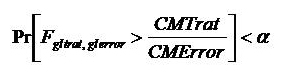
Supuestos:
Explicamos que estos supuestos deben cumplirse para que la probabilidad de error de tipo I en la prueba de F sea efectivamente igual al valor α elegido para el nivel de significación. En un par de semanas practicaremos pruebas para verificar la validez de estos supuestos.
Implementación:
Revisamos los cálculos de las sumas de cuadrados, de los grados de libertad y de los cuadrados medios para construir la tabla de análisis de la varianza.
| Fuente de Variación | Suma de Cuadrados | grados de libertad | Cuadrados Medios | CMTrat/CMError |
| Tratamientos | 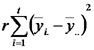 |
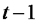 |
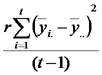 |
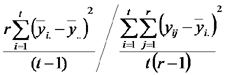 |
| Error | 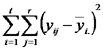 |
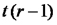 |
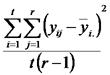 |
|
| TOTAL | 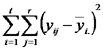 |
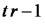 |
Revisamos el uso de las tablas de la distribución F de Snedecor para realizar la prueba basada en el cociente CMTrat/CMError.
Fundamentación:
Nos acercamos de dos maneras a la comprensón de la lógica de la prueba de hipótesis basada en el análisis de la varianza. Primero, dibujamos gráficos de dispersión que pudieran provenir de un experimento en el cual los tratamientos no tienen efecto (diferente) y de un experimento en el cual los tratamientos tienen efectos diferentes. Sobre el eje de ordenadas de esos gráficos visualizamos los diferentes tipos de desvíos que contribyen a cada una de las sumas de cuadrados y mostramos que, cuando los tratamientos tienen efectos diferentes se agranda la SCTrat pero no la SCError y por eso se agranda el cociente CMTrat/CMError. Una observación importante en este punto fue que, aún si los tratamientos no tienen efectos (diferentes), la SCTrat es habitualmente mayor que cero debido a la variación aleatroria.
En segundo término nos acercamon al fundamento de la prueba de hipótesis basada en el análisis de la varianza examinando los CMError y CMTrat para ver cuales son sus valores esperados.
En relación con CMError vimos que podemos escribirlo como:
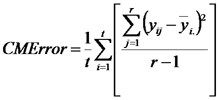
Lo que quedó entre corchetes no es otra cosa que el estimador insesgado de la varianza basado en los datos del tratamiento i. Por lo tanto, CMError es, en realidad, la media aritmética de t estimadores insesgados de σ² basados en los datos de cada uno de los tratamientos. Por eso, el valor esperado de su promedio es la varianza de los errores σ² .
![E[CME]](ecme.jpg)
Para comprender bien esto tuvimos que recordar qué es un estimador insesgado y recordar cuál es la esperanza de la media aritmética. Además, en este punto aparece cierta justificación para el supuesto de homogeneidad de varianzas. Para que la esperanza de CMError sea igual a la varianza, esta varianza tiene que ser una sola.
En relación con CMTrat vimos que podemos escribir la fórmula como:
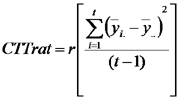
Mirando el término que queda entre corchetes, podemos reconocer la forma de un estimador insesgado de una varianza. Para que realmente lo sea es necesario que las medias de tratamientos tengan igual esperanza. Esto es lo que ocurre si los tratamientos no tienen efectos diferentes. En ese caso, lo que estima el término entre corchetes es la varianza de las medias de tratamientos que, como consecuencia del teorema dentral del limite que vimos en estadística general es igual a la varianza de las respuestas dividida por el número de repeticiones r. Por eso, cuando los tratamientos no tienen efectos diferentes, la esperanza de CMTrat es igual a la varianza. Em cambio, si los valores esperados de las medias de tratamientos difieren entre tratamientos (porque los tratamientos tienen efectos diferentes) el valor esperado de CMTrat se agranda en la medida que describe la siguiente fórmula de la esperanza de CMTrat que presentamos sin demostrar.
![E[CMT]](ecmt.jpg)
En esta fórmula se puede ver otra vez que, si los efectos de tratamientos son nulos, el valor de CMtrat es igual a la varianza de los errores.
A partir de estos resultados pudimos notar que cuando los tratamientos no tienen efectos diferentes CMTrat y CMError tienen la misma esperanza. Como consecuencia de esto, si los tratamientos no tienen efecto diferente, la esperanza del cociente CMTrat/CMError es igual a 1. En este caso, la distribución de probabilidad de este cociente es la distribución F de Snedecor. En cambio, cuando los tratamientos tienen efectos diferentes, CMTrat tiene un valor esperado mayor que el valor esperado de CMError y el valor esperado del cociente CMTrat/CMError es mayor que 1. En ese caso, la distribución de probabilidad es diferente de la F de Snedecor [no lo dijimos pero, en realidad es otra distribución que se llama F no central]. Esto justifica la prueba de F que se usa para rechazar o no la hipótesis nula que dice que los tratamientos no tienen efectos diferentes.
Pusimos a la vista la tabla de análisis de la varianza calculada con los datos del problema discutido en la clase práctica. A partir de la prueba de F se rechaza la hipótesis nula que dice que los diferentes tratamientos (momento de aplicación de fertilizante) tienen igual efecto sobre el contenido de proteína de los granos de cebada. Esta conclusión, sin embargo, es de limitada utilidad porque no especifica cuál/es tratamientos tiene/n mayor efecto.
Pasamos entonces a considerar alternativas para identificar los tratamientos con efecto diferente:
Una primera alternativa que fue propuesta es mirar y ordenar las medias aritméticas correspondientes a cada tratamiento. Esto es seguramente una buena idea, pero la comparación directa entre las medias está limitada por la falta de un criterio para decidir en qué casos las diferencias son significativas (cuándo corresponde atribuirlas a diferencias en los efectos y no al error experimental).
La segunda alternativa que consideramos era utilizar la distribución t de Student para hacer varias pruebas de hipótesis para comparar las medias de a pares. Esta alternativa fue descartada porque vimos que la probabilidad de cometer error de tipo 1 (de concluir que dos tratamientos tienen diferente efecto cuando en realidad tienen el mismo efecto) en al menos una de las comparaciones crecía con el número de comparaciones hasta valores inadmisibles. Como en el experimento analizado en la clase práctica se comparan 4 tratamientos, hay 6 pares de efectos para comparar. Si se van a hacer 6 comparaciones con la prueba de t, cada una con un nivel de significación del 5%, la probabilidad de cometer error de tipo 1 en al menos una de ellas es: 1-(1-0,05)6 = 0,265 (Recordar la distribución binomial).
Una solución es usar pruebas diseñadas para controlar la así llamada tasa de error por experimento. Con estas pruebas se busca que la probabilidad de cometer error de tipo 1 en al menos una comparación sea igual a α. En este curso presentamos una de diversas pruebas de este tipo, la prueba de Tukey.
Esta prueba se basa en la distribución de un estadístico llamado rango studentizado. La distribución de probabilidad de este estadístico bajo la hipótesis nula (ausencia de efectos) está tabulada para distintos valores del número de tratamientos y de grados de libertad del error. A partir de esta distribución se pueden calcular intervalos de confianza para las diferencias entre dos efectos i e i' como:
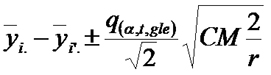
donde q es el percentil correspondiente de la distribución del rango studentizado. Siempre que el intervalo de confianza no abarque al cero se concluirá que hay diferencia entre los efectos i e i' . Por eso, al radio de este intrvalo de confianza, que es igual para todos los pares de efectos que se comparen, se lo llama DMS (mínima diferencia significativa) y se usa como regla para las comparaciones.
En la guía de problemas de Modelos Estadísticos hay una tabla que da directamente los valores de q divididos por la raiz de 2. En los libros se encuentran más comúnmente tablas de q, el rango studentizado.
Cuando llegamos a este punto, ya casi no quedaba tiempo para desarrollarlo. Por eso presentamos sólo la justificación para usar este diseño y el modelo estadístico que le corresponde. Antes de la clase práctica, los estudiantes deberán estudiar el capítulo correspondiente en la Guia de clases teóricas con especial atención a cómo se hace el análisis de la varianza en este caso.
Justificación:
Los modelos estadísticos separan la variación de las respuestas asociada con factores controlados de la variación asociada con factores no controlados. En el modelo del problema discutido en la clase práctica hay un factor controlado que corresponde a los tratamientos de aplicación de fertlizante. A los factores no controlados se les atribuye el error experimental que es una variable aleatoria.
Sin embargo, hay situaciones en las que resulta posible controlar algun factor (o grupo de factores) que no corresponde a los tratamientos (es decir que no corresponde a efectos que interese comparar) pero que, si no se lo controla, contribuye al error experimental. Controlando este tipo de factores, se intenta disminir la varianza de los errores y aumentar la capacidad del análisis para detectar diferencias en los efectos de los tratamientos.
Para realizar este tipo de experimento es necesario agrupar a las unidades experimentales en bloques homogéneos en relación con los factores en cuestión (p.ej. humedad e insolación en el experimento de sorgo visitado en la primera clase práctica) y asignar los tratamientos al azar dentro de los bloques.
Formulación del modelo:
En este caso el modelo pasa a ser:
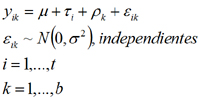
dónde t es el número de tratamientos y b es el número de bloques.
Cuando se hace un diseño en bloques, se disminuye SCError pero también se disminuye gle (grados de libertad del error). Por eso, si los bloques están justficados porque separan unidades experimentales con diferente respuesta esperada al mismo tratamiento, el valor de CMError disminuye y la prueba de F detecta diferencias menores en los efectos de los tratamientos. En cambio, si los bloque no están justificados porque en realidad no separan unidades experimentales con diferente respuesta esperada al mismo tratamiento, el valor de CMError aumenta y el la prueba F pierde potencia para detectar diferencias en los efectos de los tratamientos.
Comenzamos revisando los problemas incluidos en el examen parcial, uno referido a los factores que controlan el alargamiento de las hojas de los pastos y el otro a los factores que controlan la emisión de CO2 desde los suelos agrícolas hacia la atmósfera. Para cada uno de los dos casos:
Para discutir el diseño en bloques, examinamos el caso de un experimento con el cual se intenta evaluar los efectos de diferentes sistemas de labranza sobre la emisión esperada de CO2 utilizando como unidades experimentales a lotes agrícolas ubicados en las cuencas de diferentes arroyos de la Pampa Ondulada. Luego de explicar qué es exactamente una cuenca, dijimos que estaría justificado utilizar DBCA en lugar de DCA si la emisión esperada de CO2 de los suelos de lotes trabajados con el mismo sistema de labranza pero ubicados en diferentes cuencas fuese diferente. En casos como ese, el diseño en bloques tiene las siguentes ventajas:
Luego presentamos el análisis de la varianza correspondiente al DBCA poniendo especial atención a la suma de cuadrados de los errores.
| Fuente de Variación | Suma de Cuadrados | grados de libertad | Cuadrados Medios | CMTrat/CMError |
| Bloques |  |
 |
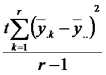 |
|
| Tratamientos | 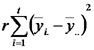 |
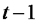 |
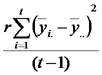 |
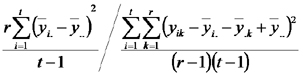 |
| Error | 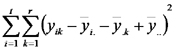 |
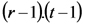 |
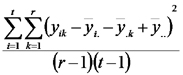 |
|
| TOTAL |  |
 |
Finalmente, enfatizamos que, cuando se analizan los datos de un experimento con DBCA, se utiliza la prueba F para poner a prueba la hipótesis de ausencia de efectos de los tratamientos sobre la respuesta esperada. En cambio, la prueba F habitualmente no puede ser utilizada para poner a prueba hipótesis sobre efectos de los bloques porque los bloques no son asignados al azar a las unidades experimentales. Las tablas de análisis de la varianza que producen los programas estadísticos presentan un cociente de cuadrados medios y un valor p para bloques porque no pueden distinguir entre un experimento en bloques y un experimento factorial (que vemos más adelante). Sin embargo, esos valores habitalmente no sirven para hacer inferencia. El viernes que viene hablaremos más sobre este tema.
Comenzamos recordando los supuestos bajo los cuales la probabilidad de error de tipo I en la prueba de la hipótesis nula de igualdad de efectos de los tratamientos basada en el análisis de la varianza es efectivamente igual al valor α elegido para el nivel de significación:
Si la probabilidad de error de tipo I es parecida al valor α elegido para el nivel de significación, decimos que la prueba es robusta. La prueba F es robusta cuando la distribución de probabilidad de los errores es exctamente igual a la Normal y cuando las varianzas difieren un poco entre tratamientos, siempre y cuando el número de repeticiones sea igual para todos los tratamientos.
Luego comentamos métodos para evaluar posibles violaciones de los 3 supuestos:
Distribución Normal de los errores:
Explicamos como se construye un Q-Q plot para evaluar si los errores son variables aleatorias con distribución Normal. Este tipo de gráfico compara los cuantiles (como percentiles, cuartiles, mediana) de la distribución Normal que se supone debería seguir la variable en cuestión con los correspondientes cuantiles de la distribución de frecuencias relativas acumuladas de esa variable en el conjunto de datos disponible. Se espera que, si cada uno de los datos es una realización independiente de una variable con la distribución Normal propuesta, los puntos del gráfico se ubiquen cerca de la recta 1:1.
Homogeneidad de Varianzas:
Comentamos primero la comparación subjetiva de los estimadores insesgados de la varianza basados en los datos de cada tratamiento (cuyo promedio es CME) y el examen del gráfico de dispersión de los residuales. Luego explicamos rápidamente en qué consiste la prueba de Levene ejercitada en la clase práctica. Como bien explicó Nahuel, el procedimiento para realizar esta prueba consiste en:
Independencia entre los errores:
Para asegurarnos del cumplimiento de este supuesto propusimos:
Soluciones:
Para concluir con el tema referido a los supuestos, consideramos las siguientes alternativas para el análisis de los datos en los casos en que los supuestos no se cumplen:
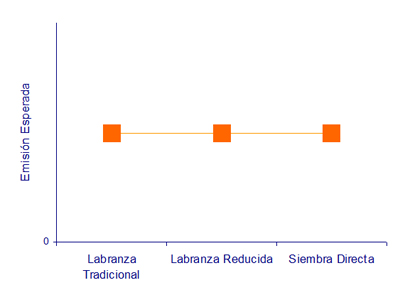
Volvimos a considerar caso de la emisión de CO2 desde el suelo hacia el aire. El modelo conceptual que habíamos desarrollado identificaba a la respiración de los organismos del suelo como la principal causa de esta emisión. Por eso propusimos que un factor que puede influir en la cantidad de CO2 emitido es la aireación del suelo que es, a su vez, modificada por el tipo de labranzas que se realicen. En ese sentido, nos planteamos las siguientes dos situaciones hipotéticas en relación con lotes cultivados con soja con diferentes sistemas de labranza:
 |
 |
| A: Estos sistemas de labranza NO tienen distintos efectos sobre la emisión esperada de CO2. | B: Estos sistemas de labranza tienen distintos efectos sobre la emisión esperada de CO2. |
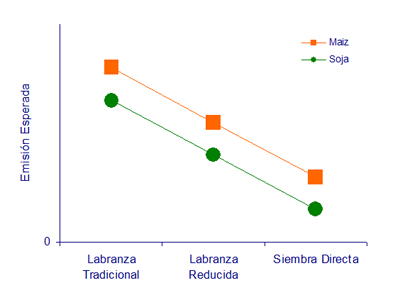
En nuestro modelo conceptual habíamos propuesto además que la cantidad y la calidad del rastrojo que se incorpora al suelo podrían influir sobre la emisión esperada de CO2. Como tanto la calidad como la cantidad del rastrojo son diferentes entre los cultivos de soja y maiz volvimos a plantear dos situaciones hipotéticas en las cuales los sistemas de labranza (tradicional, reducida y siembra directa) y los cultivos (maiz y soja) tienen diferentes efectos sobre la emisión esperada de CO2:
 |
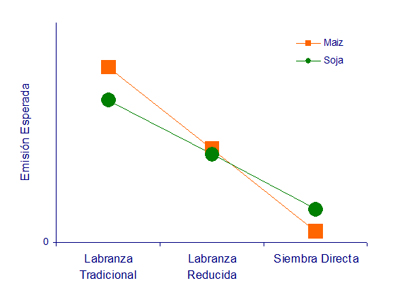 |
| C: El efecto de cada cultivo sobre la emisión esperada de CO2 es igual con los tres sistemas de labranza. El efecto de cada sistema de labranza es igual con los dos cultivos. | D: El efecto de cada cultivo sobre la emisión esperada de CO2 depende de cuál de los tres sistemas de labranza se utiliza. El efecto de cada sistema de labranza depende de cuál de los dos cultivos se realiza. |
Sobre la base de este ejemplo, presentamos la terminología necesaria para referirse a experimentos factoriales. En este caso, tipo de cultivo y sistema de labranza son dos FACTORES. Maiz y soja son dos NIVELES del factor tipo de cultivo. Labranza tradicional, labranza reducida y siembra directa son tres NIVELES del factor sistema de labranza. Realizamos un EXPERIMENTO FACTORIAL cuando asignamos al azar a cada unidad experimental una combinación de niveles de los factores. Cada combinación de niveles es un TRATAMIENTO. (Notar que hasta ahora habíamos trabajado con experimentos que incluían un solo factor. Por eso, cada tratamiento correspondía a un nivel de dicho factor).
En la situación C, la emisión esperada de CO2 es igual a la emisión promedio más dos efectos, el del tipo de cultivo y en del sistema de labranza. En cambio, en la situación D, la emisión esperada de CO2 es igual a la emisión promedio más un efecto específico de la combinación de tipo de cultivo y sistema de labranza. La manera usual de representar esto en un modelo estadístico es la siguiente:
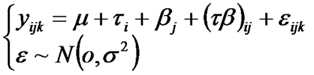
Los términos  y
y 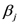 corresponden a los llamados EFECTOS PRINCIPALES y
el término
corresponden a los llamados EFECTOS PRINCIPALES y
el término  correponde al llamado
EFECTO DE LA INTERACCION entre el nivel i de un factor y el nivel
j del otro factor. En la situación C, los efectos de las
interacciones son iguales a cero y cada emisión esperada
es igual a la emisión promedio general más la
correspondiente suma de los efectos principales. En la
situación D, los efectos de las interacciones son
diferentes y, por eso, cada emisión esperada es diferente
de la emisión promedio general más la suma de los
efectos principales.
correponde al llamado
EFECTO DE LA INTERACCION entre el nivel i de un factor y el nivel
j del otro factor. En la situación C, los efectos de las
interacciones son iguales a cero y cada emisión esperada
es igual a la emisión promedio general más la
correspondiente suma de los efectos principales. En la
situación D, los efectos de las interacciones son
diferentes y, por eso, cada emisión esperada es diferente
de la emisión promedio general más la suma de los
efectos principales.
Su implementación para un caso particular:
Continuamos considerando el problema de la transferencia de carbono de la materia orgánica de los suelos agrícolas hacia la atmósfera. Imaginamos que el presidente del INTA, preocupado por la pérdida de fertilidad de los suelos de la Pampa Ondulada, y el ministro de Medio Ambiente, preocupado por el aumento de la concentración de CO2 de la atmósfera, se reunen para encargar a un equipo formado por un ingeniero agrónomo y un licenciado en ciencias ambientales egresados de la FAUBA que estudien los posibles efectos de dos diferentes cultivos (soja y maiz) y de 3 diferentes sistemas de labranza (tradicional, reducida, siembra directa) sobre la emisión esperada de CO2 del suelo y discutimos cuál sería el procedimiento que podrían seguir estos profesionales. El procedimiento que propusimos es el siguiente:
En relación con este procedimiento, nos detuvimos en los criterios para decidir el número de repeticiones de cada tratamiento. Vimos que estos criterios son:
Con cada nivel de significación, cuanto mayor sea la varianza de los errores y cuanto más pequeños sean los efectos que interesa detectar mayor será el número de repeticiones necesario.
Modelo, efectos simples, efectos principales, efectos de interacciones:
El modelo que corresponde al experimento que propusimos es el siguiente:
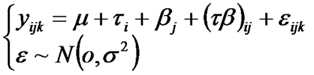
i=1 corresponde a cultivo de soja y i=2 corresponde a maiz:
j=1 corresponde a labranza tradicional, j=2 a labranza reducida y j=3 a siembra directa.
Examinando el modelo, identificamos a los valores esperados de emisión de CO2 correspondientes a cada tratamiento, a los efectos simples de cada nivel de cada factor dado el nivel del otro factor, a los efectos principales de cada nivel de cada factor y a los efectos de la interacción.
Por ejemplo:
El VALOR ESPERADO de la emisión de CO2 de un lote cultivado con soja con labranza reducida es,
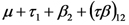
El EFECTO SIMPLE del cultivo de maiz en un lote trabajado con siembra directa es,
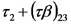
El EFECTO SIMPLE de la labranza tradicional en un lote cultivado con soja,

Si los efectos simples de la labranza tradicional en los lotes cultivados con soja son iguales que en los lotes cultivados con maiz, tenemos que,
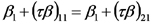
y, por lo tanto,

Si los efectos simples de cada uno de los tres sistemas de labranza sobre la emisión esperada de CO2 son iguales entre cultivos, decimos que no hay EFECTO DE INTERACCION entre los tres sistemas labranza y los dos cultivos.
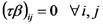
ANOVA para un experimento factorial DCA:
Explicamos que en el caso de los experimentos factoriales, el análisis de la varianza permite particionar la suma de cuadrados de los tratamientos en partes correspondientes a cada uno de los efectos principales y a la interacción.
Igual que en el análisis de varianza de una vía que desarrollamos en las semanas anteriores, el desvío de una respuesta observada respecto de la media general puede ser particionado en dos partes, una correspondiente al efecto de factores no controlados (el desvío de la respuesta observada respecto de la media del tratamiento corespondiente) y otra correspondiente a la estimación del efecto del tratamiento correspondiente (el desvío del promedio del tratamiento correspondiente respecto de la media general) .
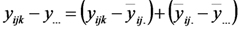
A su vez, el desvío del promedio de un tratamiento (combinación de niveles de los dos factores) respecto de la media general puede ser particionada en tres componentes, el desvío del promedio de todas las respuestas observadas para el nivel correspondiente del primer factor respecto de la media general, el desvío del promedio de todas las respuestas observadas para el nivel correspondiente del segundo factor respecto de la media general, y un complemento que constituye la estimación del efecto de la interación correspondiente.
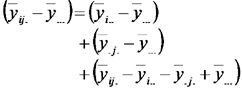
Las sumas de cuadrados de esos desvíos constituyen el análisis de la varianza de un experimento factorial con diseño completamente aleatorizado (DCA).
| Fuente de Variación | Suma de Cuadrados | grados de libertad | Cuadrados Medios | Cociente |
| Modelo (tratamientos) |  |
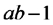 |
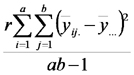 |
|
| Fact1 | 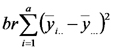 |
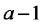 |
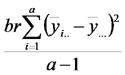 |
|
| Fact2 | 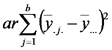 |
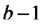 |
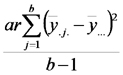 |
|
| Interacción Fact1*Fact2 | 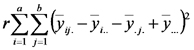 |
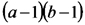 |
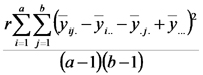 |
|
| Error | 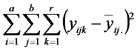 |
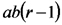 |
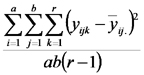 |
|
| TOTAL |  |
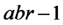 |
Notar que la suma de cuadrados de los tratamientos es igual a la suma de cuadrados asociada al factor 1 más la suma de cuadrados asociada al factor 2 más la suma de cuadrados asociada con las interacciones. Lo mismo ocurre con los grados de libertad. El cociente entre cuadrado medio de los tratamientos (llamado también del modelo) y cuadrado medio del error sirve para poner a prueba la hipótesis nula general que dice que las distintas combinaciones de niveles de los factores tienen igual efecto sobre la respuesta esperada (emisión de CO2).
ANOVA para un experimento factorial DBCA:
Si es posible controlar parte de la heterogeneidad entre unidades experimentales que contribuye a los error experimentales en el modelo anterior entonces es mejor usar un diseño en bloques. Por ejemplo, puede ser que parte de la heterogeneidad entre los lotes del experimento esté relacionada con diferencias entre establecimientos manejados por diferentes empresas. En ese caso, los lotes son clasificadas en bloques por establecimiento y los tratamientos son asignados al azar a los lotes dentro de cada bloque. (en cada bloque están todos los tratamientos).
El modelo pasa a ser:
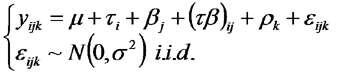
En el análisis de la varianza correspondiente a este diseño, las fórmulas de las sumas de cuadrados, grados de libertad y cuadrados medios correspondientes al modelo (tratamientos), a los efectos principales y de la interacción son idénticas a las del factorial DCA.
En cambio, se introduce la la suma de cuadrados asociada con bloques y se modifican la suma de cuadrados, los grados de libertad y el cuadrado medio de los errores.
| Fuente de Variación | Suma de Cuadrados | grados de libertad | Cuadrados Medios | Cociente |
| Modelo (tratamientos) |  |
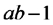 |
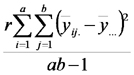 |
|
| Fact1 | 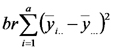 |
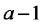 |
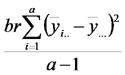 |
|
| Fact2 | 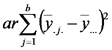 |
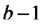 |
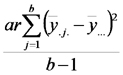 |
|
| Interacción Fact1*Fact2 | 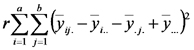 |
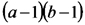 |
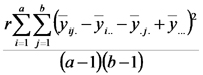 |
|
| Bloques | 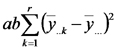 |
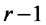 |
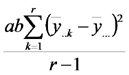 |
|
| Error | 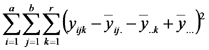 |
 |
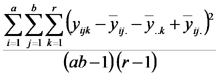 |
|
| TOTAL |  |
 |
Pruebas de hipótesis y comparaciones múltiples en experimentos factoriales:
Antes de desarrollar las tablas de análisis de la varianza habíamos discutido el siguiente procedimiento para poner a prueba hipótesis acerca de los efectos en un experimento factorial:
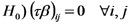
En nuestro ejemplo, esta hipótesis significa que los efectos simples de cada cultivo ensayado sobre la emisión esperada de CO2 son iguales para los tres sistemas de labranza y que los efectos de cada sistema de labranza ensayado son iguales para cada uno de los dos cultivos.
Dicho de otro modo, la hipótesis nula propone que los efectos simples de los dos cultivos probados no dependen del sistema de labranza y que los efectos simples de los tres sistemas de labranza probados no dependen de cual de los dos cultivos se haga.
Otra manera de expresar esta hipótesis nula es decir que no hay efecto de la interacción entre cultivo y sistema de labranza sobre la emisisón esperada de CO2.
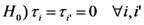
Bajo la hipótesis de ausencia de efectos de interacción, esta hipótesis nula significa que los efectos principales de los cultivos probados son iguales (nulos). Es decir que significa que dado un sistema de labranza la emisión esperada de CO2 no difiere entre cultivos.
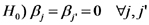
Bajo la hipótesis de ausencia de efectos de interacción, esta hipótesis nula significa que los efectos principales de los sistemas de labranza probados son iguales (nulos). Es decir que significa que dado un cultivo la emisión esperada de CO2 no difiere entre sistemas de labranza.
Revisión del análisis de regresión simple:
Concentramos nuestra atención en los factores que afectan a la productividad primaria neta de la vegetación, la diferencia entre la cantidad de materia (y energía) que las plantas incorporan por la fotosíntesis y la cantidad que pierden por la respiración. Este es el tema del problema que se discutirá en la próxima clase práctica (Trabajo Domiciliario: Problema 2). Entre los factores mencionamos a la disponibildad de agua en el suelo, que a su vez depende de la cantidad de lluvias, de la infiltración, de la características del suelo que hacen a la retención del agua, a la cantidad de luz incidente, a la capacidad de la vegetación para interceptar a la luz, a la disponibilidad de nutrientes esenciales como el nitrógeno, a la temperatura y a cayacterísticas de las plantas relaconadas con su eficiencia en el uso del agua, la luz y los nutrientes. Apoyados en este modelo conceptual interpretamos las diferentes partes de un modelo de regresión lineal simple que representa la relación estadística que existe entre la productividad primaria neta de las estepas (PPN) y la lluvia anual que reciben.
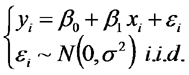
En el modelo:
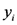
representa la PPN en el i-esimo sitio de estepa y
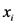
representa la lluvia anual en el i-esimo sitio de estepa.
La cantidad
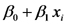
representa la PPN esperada en un sitio de estepa con lluvia anual igual a xi tomado al azar.
Finalmente, la cantidad
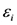
representa la diferencia entre a PPN que efectivamente ocurre en un sitio de estepa tomado al azar y su PPN esperada. Esta cantidad es una variable aleatoria que puede depender en parte de los restantes factores que mencionamos en el modelo conceptual.
Revisión de la estimación de los parámeros y de la prueba de hipótesis en el análisis de regresión simple:
A continuación recordamos el procedimiento para estimar los parámetros de este modelo. El estimador de la pendiente es:
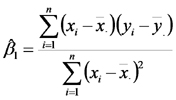
El estimador de la ordenada al origen es:
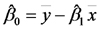
El estimador de la varianza de los errores es:
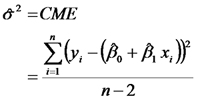
Para poner a prueba la hipótesis nula que dice que la PPN esperada de una estepa no varía con la cantidad de lluvia por anual,
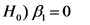
Seleccionamos un nivel de significación α y rechazamos la hipóesis nula siempre que,

Análisis de Varianza para modelos de regresión:
Para finalizar, presentamos el análisis de la varianza correspondiente al modelo de regresión lineal simple y mostramos que la prueba F de la hipótesis nula que dice que no hay efectos de la lluvia sobre la PPN es equivalente a la prueba t que acabamos de recordar. El análisis de la varianza correspondiente es:
| Fuente de Variación | Suma de Cuadrados | grados de libertad | Cuadrados Medios | Cociente |
| Modelo | 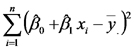 |
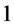 |
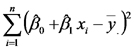 |
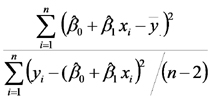 |
| Error | 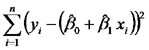 |
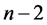 |
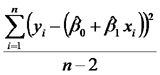 |
|
| TOTAL | 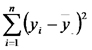 |
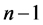 |
Si ponemos atención en el cociente de cuadrados medios, podemos ver que el numerador, que es igual a la suma de cuadrados del modelo puede ser escrito como:
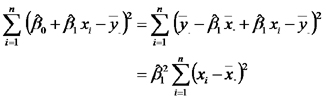
Es decir que el cociente de los cuadrados medios puede ser escrito como:
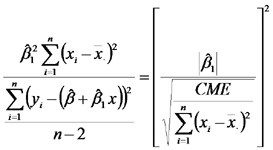
en donde se ve que el cociente de cuadrados medios es igual al cuadrado del estadístico de la prueba t. Las pruebas de F y de t conducen a idénticas conclsiones acerca de la hipótesis nula que dice que la PPN esperada no es diferente entre sitios de estepa con diferente lluvia anual.
La razón que tenemos para presentar la prueba basada en la distribución F es que se puede aplicar a modelos de regresión más complicados, los llamados MODELOS DE REGRESION MULTIPLE. Estos modelos permiten incluir la posible influencia de más de una variable regresora sobre la esperanza de la variable respuesta.
Nos concentramos en el caso de la relación estadística entre la productividad primaria neta de las estepas (PPN) y dos factores relacionados con su régimen de humedad: la cantidad de lluvia anual (PMA) y la capacidad de retención hídrica del suelo (CRH). Para comenzar, recordamos la formulación del modelo de regresión lineal simple que relaciona la PPN con la lluvia anual discutido en la clase pasada y el uso del análisis de la varianza para poner a prueba la hipótesis nula que dice que las diferencias en la lluvia anual no tienen efecto sobre la PPN esperada.
A partir de este punto, ampliamos nuestro modelo de regresión a uno que considera dos variables independientes: la lluvia anual (PMA) y la capacidad de retención hídrica del suelo (CRH).
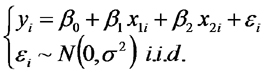
En el modelo:
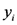
representa la PPN en el i-esimo sitio de estepa,
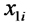
representa la PMA en el i-ésimo sitio de estepa y
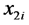
representa la CRH del suelo en el i-ésimo sitio de estepa.
La cantidad
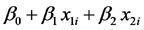
representa la PPN esperada en un sitio de estepa con lluvia anual igual a x1i y con capacidad de retención hídrica del suelo igual a x2itomado al azar. La cantidad
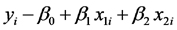
representa el desvío entre a PPN que efectivamente ocurre en un sitio de estepa tomado al azar y su PPN esperada.
Los parámetros
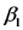 y
y 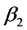
son los denominados COEFICIENTES DE REGRESION PARCIAL. Cada uno de estos parámetros mide el cambio en la PPN esperada asociado con un cambio unitario en una de las variables independientes cuando la otra variable independiente permanece constante.
Diferencia entre los coeficientes de regresión parcial y los coeficientes de regresión total:
Nos detuvimos a enfatizar que los coeficientes de regresión parcial estimados son muchas veces diferentes de los coeficientes de regresión de los modelos de regresión lineal simple que incorporan sólo a la variable predictora correspondiente. Usando gráficos de dispersión, mostramos que esto ocurre cuando las variables predictoras no son completamente independientes entre si en el conjunto de dats. En el modelo de regresión lineal simple que tiene a la PMA como la variable predictora, el coeficiente de regresión (total) estimado etima el cambio en la PPN esperada asociado con un cambio unitario en la PMA que puede venir acompañado por un cambio en la CRH. En este sentido, es distinto del correpondiente coeficiente de regresión parcial del modelo de regresión múltiple que estima el cambio en la PPN esperada asociado con un cambio unitario en la PMA para un valor dado de CRH.
Modelo de regresión múltiple con interacción:
A propósito de las preguntas de Nadia y de Cristóbal presentamos un modelo de regresión múltiple con un término de interacción y lo comparamos con el modelo anterior que no incluye la posibilidad de que los efectos de una de las variables predictoras sobre la esperanza de la variable respuesta varíen con otra variable predictora.
El modelo con dos variables predictoras e interacción es:
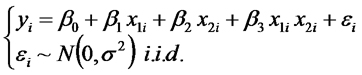
donde el coeficiente de regresión parcial beta 3 que multiplica al producto de las dos variables predictoras es el correspondiente a la interacción. Para comprender cómo es que este coeficiente mide el efecto de la interacción, escribimos el valor esperado de la variable respuesta reagrupando los términos como sigue:

De ese modo podemos ver que la pendiente del plano de regresión en la dirección de x1 varía según cuál sea el valor que toma x2. En otras palabras, el efecto de un cambio unitario de x1 sobre el valor esperado de y depende del valor de x2.
Para ilustrar este caso, comentamos que se ha visto que, cuando se considera la diferente vegetación que vive a lo largo de un rango amplio de valores de lluvia anual, se encuentra que el efecto de las diferencias en capacidad de retención hídrica sobre la PPN esperada varía según cuánto llueva. En lugares extremadamente áridos, la vegetación de suelos con mayor capacidad de retención hídrica (que son los más arcillosos) tiene menor PPN que la vegetación asociada con suelos con menor capacidad de retención hídrica (que son menos arcillosos). En cambio, en áreas de clima húmedo la vegetación tiene mayor PPN cuando crece en suelos con mayor capacidad de retención hídrica. Este fenómeno es conocido como efecto inverso de la textura.
Para estimar los parámetros del modelo de regresión múltiple se utiliza el método de mínimos cuadrados del mismo modo que para estimar los parámetros del modelo de regresión lineal simple. Es decir que los estimadores de
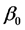 ,
, 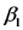 y
y 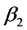
son los valores que hacen mínima la siguiente suma de cuadrados de los residuales:
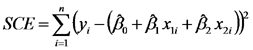
En este punto, nos detuvimos para remarcar que, por primera vez en los cursos de Estadística General y de Modelos Estadísticos, omitimos presentar las fórmulas de los estimadores. Esta diferencia en la profundidad con la cual presentamos este tema se debe a que las fórmulas de los estimadores de mínimos cuadrados de los coeficientes de regresión parcial varían según cuántas variables predictoras se incorporen en el modelo de regresión múltiple. Existen fórmulas generales que se expresan en el lenguaje de álgebra de matrices cuya presentación excede el nivel de este curso pero que se pueden aprender en cursos más avanzados que en esta facultad se dictan en la Escuela para Graduados. Por el momento, obtendremos los estimadores utilizando programas de análisis estadístico que resuelven (de alguna manera) el problema de minimizar la suma de cuadrados de los residuales.
Primero consideramos la tabla de análisis de la varianza obtenida a partir de la estimación de los parámetros del modelo de regresión múltiple presentado más arriba con los datos del problema 2 del trabajo práctico domiciliario.
| Fuente de Variación | Suma de Cuadrados | grados de libertad | Cuadrados Medios | Cociente | Valor p |
| Modelo | 38227,59 | 2 | 19113,80 | 61,12 | <0,0001 |
| Lluvia | 34345.46 | 1 | 34345,46 | 109,82 | <0,0001 |
| Capacidad de retención hídrica | 3321,79 | 1 | 3321,79 | 10,62 | 0,0036 |
| Error | 6880,17 | 22 | 312,73 | ||
| TOTAL | 45107,76 | 24 |
En esta tabla, el cociente de cuadrados medios de la linea resaltada en verde permite poner a prueba la hipótesis nula global que dice que la PPN esperada no varía con la lluvia anual ni tampoco con la capacidad de retención hídrica del suelo.
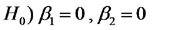
Los cuadrados medios de las líneas resaltadas en amarillo permiten poner a prueba hipótesis nulas particulares referidas a los coeficientes de regresión parcial. En la primera linea amarilla se pone a prueba la hipótesis nula
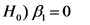
que establece que sitios con un mismo valor de CRH del suelo y diferente lluvia anual tienen igual PPN esperada. En la seguda línea amarilla se pone a prueba la hipótesis nula

que establece que sitios con un mismo valor de lluvia anual y diferente CRH del suelo tienen igual PPN esperada.
Sumas de cuadrados parciales:
Las sumas de cuadrados correspondientes de las líneas resaltadas en amarillo son las SUMAS DE CUADRADOS PARCIALES. Estas sumas no constituyen una partición de la suma de cuadrados del modelo en porciones aditivas (es decir que su suma es diferente de la suma de cuadrados del modelo).
Cada una de estas sumas de cuadrados parciales mide la variación de la variable respuesta no explicada por la/s otra/s variable/s predictora/s incluidas en el modelo que sí es explicada por la variable en cuestión. Por ejemplo:
Cálculos de las sumas de cuadrados:
Las sumas de cuadrados total, del modelo y del error son similares a las correspondientes en todos los modelos que vimos anteriormente.
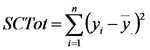
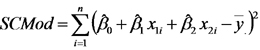
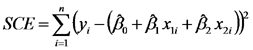
En cambio, cada sumas de cuadrados parcial se calcula como la diferencia entre la suma de cuadrados del modelo (esto es la suma de cuadrados del modelo completo) y la suma de cuadrados de un modelo que incluye a todas las variables del modelo completo menos la variable en cuestión. Por ejemplo, la suma de cuadrados parciales de la primera línea resaltada en amarillo es la diferencia entre la suma de cuadrados del modelo completo (que está en la línea resaltada en verde) y la suma de cuadrados de un modelo de regresión lineal simple cuya variable predictora es la CRH del suelo.
La suma de cuadrados de este modelo reducido como
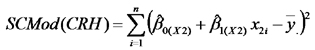 ,
,
donde los subíndices de los coeficientes estimados resaltan que son diferentes de los estimados para el modelo completo. Entonces la suma de cuadrados parcial de la primera línea resaltada en amarillo es:
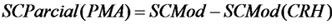
Como vimos, los coeficientes de regresión parcial pueden ser diferentes de los coeficientes de regresión de un modelo reducido que no incluye todas las variable predictoras. Tambien vimos que las sumas de cuadrados parciales en general no suman la suma de cuadrados del modelo. Como dijimos, esto se debe a que habitualmente las variables predictoras no varían independientemente. Cuando la dependencia entre las variables predictoras es muy fuerte aparece el problema de multicolinealidad.
Para explicar en qué consiste este problema comenzamos por considerar el siguiente caso extremo de dependencia:
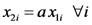
La segunda variable predictora es igual a la primera multiplicada por una constante en todas las unidades experimentales incluidas en el análisis. Para este caso, demostramos que la suma de cuadrados del modelo completo es igual a la suma de cuadrados de cualquiera de los modelos reducidos en los cuales una de las variables predictoras es excluído. Como consecuencia, las sumas de cuadrados parciales son iguales a cero.
En los casos habituales del problema de multicolinealidad, la dependencia entre las variables predictoras determina que una sea, si no exáctamente proporcional a la otra, aproximadamente proporcional a la otra.
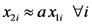
En ese caso, las sumas de cuadrados parciales son pequeñas aún cuando la suma de cuadrados del modelo puede ser alta. Esto lleva a situaciones aparentemente contradictorias en que se rechaza la hipótesis nula global que dice que ninguno de los coeficientes de regresión parcial es diferente de cero y se concluye que al menos uno de ellos es diferente de cero, pero por el otro lado pero, sin embargo, no se rechaza ninguna de las las hipótesis nulas específicas que dicen que cada uno de estos coeficientes es igual a cero.
En realidad, este problema ocurre porque, cuando las variables predictoras son estrechamente interdependientes, el conjunto de datos no contiene información suficiente para estimar qué pasa con la respuesta esperada cuando cambia una de las variables predictoras pero no cambia la otra(es decir para estimar los coeficientes de regresión parcial) porque esto no fué registrado. Como vimos, cualquiera de los modelos de regresión simple permite estimar el efecto sobre el valor esperado de la variable respuesta de un cambio unitario de una de las variables predictoras acompañado del cambio la variable predictora restante que venga asociado. Cuando el conjunto de datos presenta multicolinealidad, es hasta ese punto que puede llegar nuestro análisis.
Si tenemos interés en estimar los coeficientes de regresión parciales necesitaremos conseguir datos de la variable respuesta en unidades experimentales para las cuales los valores de las variables predictoras no cumplan con la relación de proporcionalidad que mantenían las del conjunto de datos con multicolinealidad.
El trabajo práctico de la semana 7 será realizado en un laboratorio de cómputos (del CSI o de la EPG según el turno). Para prepararse, los alumnos deberán,
Durante la primera parte de la clase volvimos a revisar el modelo de regresión lineal múltiple. Escribimos otra vez un modelo con dos variables predictoras y sin interacción,
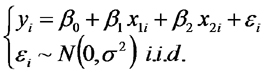
y repasamos los siguientes aspectos de su uso e interpretación:
Luego agregamos al modelo un término correspondiente a la interacción,
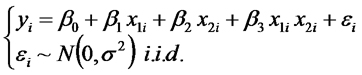
y vimos que esto no modifica el procedimiento general de análisis. Simplemente se agrega una línea a la tabla de análisis de la varianza donde se pone la suma de cuadrados parcial correspondiente al efecto de la interacción que se calcula como la diferencia entre la suma de cuadrados del modelo completo y la suma de cuadrados del modelo reducido por eliminación del término de interacción. Notar que en esta tabla las restantes sumas de cuadrados son diferentes de las de una tabla construida para analizar el modelo sin interacción.
A la pregunta de Rodrigo acerca de la similitud o diferencia entre este modelo y un modelo factorial, respondimos:
Rodrigo también preguntó si es que siempre hay que incluir el término de interacción en un modelo de regresión múltiple. A eso contestamos que no hay una respuesta general sino que la decisión de hacerlo o no se basa en cada caso en nuestra comprensión del fenómeno bajo estudio, se basa en el Modelo Conceptual.
No lo mencionamos en la clase, pero vale la pena notar que para cualquiera de los modelos que estudiamos en el curso se puede medir qué proporción de la variación observada en la variable respuesta es explicada por la variación observada en las variables predictoras mediante el estadístico R2, el cociente entre la suma de cuadrados del modelo y la suma de cuadrados totales.
Modelos de regresión lineal para respuestas curvilíneas:
Consideramos el ejemplo de la relación estadística entre la temperatura y la tasa de fotosíntesis presentado por el problema 2 del trabajo práctico de esta semana. Con los datos del problema construimos el siguiente gráfico de dispersión:
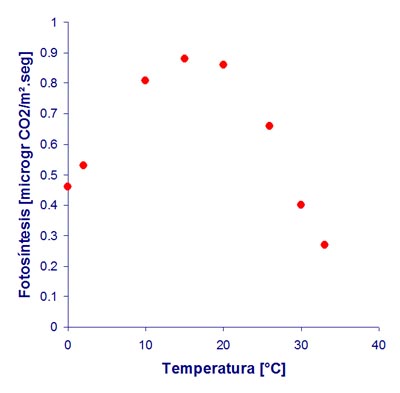
Primero explcamos que datos como estos se obtienen asignando al azar diferentes temperaturas a diferentes hojas para luego medir su tasa de fotosíntesis como el ritmo con que la concentración de CO2 disminuye en una camarita transparente en la cual se encierra a la hoja. Luego describimos verbalmente la relación estadística que se visualiza en el gráfico de dispersión entre la tasa de fotosíntesis y la temperatura. En este sentido dijimos que cuando la temperatura es baja, la tasa de fotosíntesis esperada aumenta con los aumentos de temperatura, en cambio, cuando la temperatura es alta, la tasa de fotosíntesis disminuye con los aumentos de temperatura. Esta relación se expresa en el gráfico como una línea aproximadamente parabólica que representa un tipo de respuesta llamada respuesta de óptimo. Para evaluar y documentar esta relación proponemos el siguiente modelo:
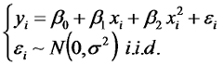
Nos detuvimos a notar que este modelo puede ser analizado como un modelo de regresión múltiple con dos variables predictoras en el cual la segunda variable predictora es igual al cuadrado de la primera. Por eso, este modelo puede ser ajustado usando un programa de análisis estadístico que ajuste un modelo de regresión lineal múltiple simplmente presentándole una segunda variable predictora que calculamos previamente como el cuadrado de la temperatura
La estimación de los parámetros y las pruebas de hipótesis se hacen exactamente del mismo modo que cuando se analiza un modelo de regresión múltiple con dos variables predictoras que no estan relacionadas funcionalmene.
Para interpretar los coeficientes de regresión parcial de este modelo conviene considerar el valor esperado de la variable respuesta (tasa de fotosíntesis) y la derivada de dicho valor esperado respecto de la variable predictora (temperatura):
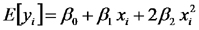
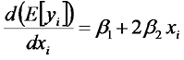
De este modo podemos apreciar que, en nuestro ejemplo:
Nadia preguntó cómo se hace para decidir si uno usa un modelo de regresión con respuesta curvilínea o un modelo de regersión lineal sin respuesta curvilínea (por ejemplo un model de regresión lineal simple). En este caso también la decisión se basa en el Modlo Conceptual, en nuestra idea del fenómeno tenemos bajo estudio.
Este modelo polinómico es un caso particular de la aplicación de transformaciones de una variable independiente para construir modelos de regresión lineal que permitan representar respuestas esperadas curvilíneas. Con la transformación cuadrática modelamos una respuesta esperada que guarda una relación parabólica con la variable predictora. Otros modelos de esta índole que mostramos son:
En todos estos modelos, la esperanza de la variable respuesta es una función lineal de los parámetros (aunque no sea una función lineal de las variables predictoras). Por eso pertenecen al conjunto de los llamados modelos de regresón lineal.
Los modelos de regresión no lineal que aparecen entre las opciones que ofrece Infostat y otros programas de análisis estadístico son diferentes de los que presentamos en este curso. En ellos el valor esperado de la variable respuesta es una función no lineal de los parámetros (por ejemplo del logarimo de beta 0).
Modelos de regresión con variables categóricas (dummy) y ANCOVA:
Consideramos el ejemplo de los efectos de las diferencias de lluvia sobre los rendimientos esperados de dos diferentes cultivares híbridos de maiz que presentamos en el problema 3 del trabajo práctico de esta semana. Con los datos del problema construimos el siguiente gráfico de dispersión:
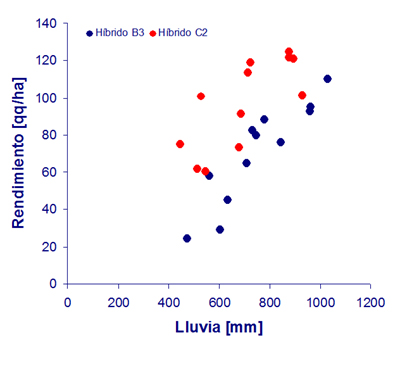
En relación con este problema, interesa saber:
Para examinar esta cuestión construimos un modelo de regresión múltiple en el cual una variable predictora es la lluvia (variable contínua) y la otra variable predictora es una variable Z que definimos así:
Zi = 0 cuando el híbrido es B3
Zi = 1 cuando el híbrido es C2
En ingles, se llama a este tipo de variables dummy porque son variables que representan lo que no son. Dummy es un espantapájaros, que parece un hombre pero no es un hombre). Una variable dummy es una variable que parece contínua pero que no lo es.
El modelo que proponemos es:
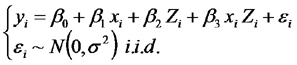
Como este es un modelo de regresión lineal múltiple, los procedimientos para la estimación de los parámetros y para la construcción de pruebas de hipótesis (basadas en el análisis de la varianza) son los mismos que ya hemos visto para otros modelos de regresión múltiple. Por eso, no volvimos a discutirlos y nos concentramos en la interpretación de los parámetros y en la secuencia correcta de pruebas de hipótesis:
En términos de nuestro ejemplo, la hipótesis
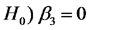
significa: las diferencias en lluvia tienen el mismo efecto sobre el rendimiento esperado del híbrido B3 y del híbrido C2. Esta es la hipótesis referida a la interacción.
La hipótesis
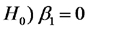
significa: las diferencias en lluvia no afectan al rendimiento esperado del híbrido B3. Si la combinamos con la hipótesis anterior, las dos juntas significan: las diferencias en lluvia no afectan al rendimiento esperado de estos híbridos. Se trata de una afirmación referida al efecto principal de la lluvia.
La hipótesis
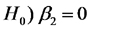
tiene interés cuando es cierta la hipótesis nula de la ausencia de efecto de la interacción. En este caso significa: los rendimientos esperados de los dos híbridos son iguales para cualquier valor de lluvia.
El parecido entre este modelo y un modelo factorial es muy notable. La diferencia más importante es que en este caso uno de los factores opera como una variable contínua con infinitos niveles. La manera en que hemos modelado la variable respuesta en este caso fue proponer un modelo de regresión al cual le presentamos la variable categórica (híbrido) como si fuera contínua.
Un enfoque alternativo se basa es construir un modelo en donde presentamos a la variable categórica tal y como la hemos presentado en los modelos que llamamos modelos de análisis de varianza y a la variable contínua del mismo modo que en los llamados modelos de regresión. Estos modelos habitualmente no incluyen el término de interacción (se basan en el supuesto de que no hay efecto de interacción) y se llaman modelos de análisis de covarianza (ANCOVA). Su formulación es la siguiente:
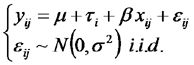
Este modelo es equivalente a un modelo con una variable dummy y sin el término de interacción.
En este punto termina el desarrollo de los temas previstos para el curso de Modelos Estadísticos. Con esto culmina una etapa comenzada con el curso de Estadística General durante la cual se presentaron los conocimientos de estadística que se espera que tenga cualquier graduado de las carreras que requieren estos cursos. Muchos estudiantes van a aprender más estadística durante el resto de sus carreras, en especial en el ciclo de intensificación y en su formación de post-grado científica o profesional. Igualmente en este punto es oportuno, alzar un poco la vista para discutir algunas cuestiones que hacen a la articulación de los métodos estadísticos en el proceso de generación del conocimiento.
Modelo conceptual y modelo estadístico:
Como hemos visto, un modelo conceptual es una expresión organizada de nuestra explicación de un fenómeno de interés. Un modelo estadístico es la expresión formal de una afirmación acerca de la distribución de probabilidad de una variable aleatoria. Para discutir las vinculaciones entre modelo conceptual y modelo estadístico volvimos a considerar el fenómeno de la transferencia de carbono desde los suelos a la atmósfera, que debería ser de interés tanto para profesionales de la agronomía como de las ciencias ambientales. En relación con este fenómeno, formulamos un modelo conceptal sencillo y un modelo estadístico relacionado que aparecen resumidos en la figura:
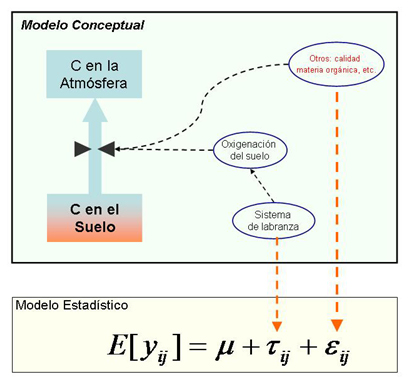
Luego examinamos las conclusiones a las que arribamos si el análisis de la varianza basado es este modelo estadístico conduce a rechazar la hipótesis nula que dice que no hay diferencias significativas entre los promedios de emisión de carbono observados para los diferentes tratamientos:
El análisis estadístico tiene asociada una medida (basada en el nivel de significación alfa) relacionada con la seguridad que podemos sentir respecto de la conclusión tal como se enuncia en términos del modelo estadístico. Las posibles críticas a esta conclusión estarán relacionadas con el procedimiento experimental (repeticiones, aleatorización, independencia) y de análisis (nivel de significación elegido) pero difícilmente provengan de la consideración directa del modelo conceptual con el cual explicamos el fenómeno bajo estudio.
La conclusión presentada en términos del modelo conceptual, en cambio, no cuenta con una medida de la confianza que merece pero ahonda más en el fenómeno que nos interesa comprender. La crítica que hagamos de esta última conclusión provendrá de nuestra revisión de la conherencia del modelo conceptual y de la incorporación de nuevos elementos a dicho modelo conceptual. Para nuestro ejemplo podríamos preguntarnos: ¿y si las diferencias en la emisión de C de los suelos trabajados con diferente sistema de labranza fuese en realidad el resultado, no de diferencias en la oxigenación del suelo, sino de diferencias en la composición de la biota del suelo?
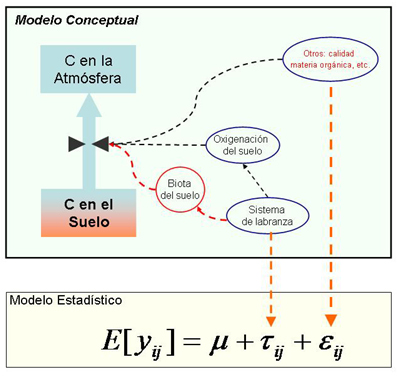
Esta crítica no proviene del análisis estadístico sino del análisis teórico. Para resolver el dilema planteado habrá que diseñar un estudio basado en un modelo estadístico apropiado. Con este ejemplo intentamos mostrar que:
Los modelos estadísticos no reeemplazan en ningún caso a los modelos conceptuales con los cuales explicamos la realidad sino que son herramientas de las que nos valemos para evaluar alternativas que surgen de analizarlos críticamente.
Efecto Estadístico y Efecto Material:
Durante el curso de Modelos Estadísticos hemos estado hablando profusamente de efectos. Ahora vale la pena que nos detengamos brevemente a distinguir el significado de la palabra efecto en el contexto en el que la hemos estado usando de los Efectos que provienen de una causa material.
A veces, los efectos estadísticos se corresponden cercanamente con Efectos materiales, otras veces se corresponden lejánamente y a veces sencillamente no se corresponden con ningun Efecto material. Veamos algunos ejemplos:
Un experimento manipulativo en el cual se evalúa la descomposición de la materia orgánica del suelo el lotes cultivados con diferentes sistemas de labranza asignados al azar. Es razonable interpretar que los efectos estadísticos que se detecten en las tasas de descoposición de la materia orgánica se corresponden con efectos materiales de los diferentes sistemas de labranza. Los sistemas de labranza son una causa material más o menos distante (puede estar mediada por diferentes efectos intermedios) de las diferencias que observemos.
Un estudio observacional de la relación estadística entre la lluvia anual y la productividad primaria de la vegetación. Los efectos estadísticos de la lluvia pueden o no corresponder a Efectos materiales de la lluvia. No hay manera de descartar la alternativa de que se deban a Efectos materiales de algun factor que varía junto con la lluvia.
Un estudio basado en un modelo factorial. El efecto de la interacción es un efecto estadístico que no tiene entidad material. No existe como un Efecto material separado en la realidad. Por ejemplo, es posible evaluar por separado los efectos de diferentes sistemas de labranza sobre la descomposición de la materia orgánica del suelo sin manipular el factor cultivo. También es posible evaluar por separado los efectos de diferentes cultivos sobre el mismo proceso sin manipular el factos sistema de labranza. Sin embargo no es posible evaluar por separado el efecto de la interacción sin manipular los factores cultivo y sistema de labranza.
Es importante distinguir el modelo estadístico de la realidad material que se estudia.
Generalización de los resultados del análisis estadístico:
Desde que comenzamos con el curso de Estadística General y hasta ahora mantuvimos una regla inamovible para determinar los límites que existen para la generalización de los resultados. La regla es esta:
Consideramos válidos a los resultados de nuestro análisis dentro de la población de la cual se tomó la muestra. La población a la cual nos referimos está formada por todas las unidades experimentales que podían haber sido incluidas en el estudio.
Desde la perspectiva de los modelos estadísticos, esta es la regla. La generalización de los resultados está basada en una medida numérica del nivel de confianza o de la probabilidad de cometer error de tipo I.
Desde la perspectiva de los modelos conceptuales, en cambio, la generalización de los resultados se basa en el análisis de cada caso basado en la comprensión que se tenga del fenómeno.
Por ejemplo, para estudiar los efectos de tres sistemas de labranza sobre la descomposición de la materia orgánica se hace un experimento en lotes tomados al azar de la cuenca del Río Arrecifes. Se encuentra que la tasa de descomposición difiere significativamente entre lotes cultivados con diferentes sistemas. La conclusión pura y dura es que: en la cuenca del Río Arrecifes, los diferentes sistemas de labranza tienen diferente efecto sobre la descomposición de la materia orgánica. El nivel de significación elegido para la prueba nos orienta respecto de cuan seguros podemos estar acerca de esa conclusión.
Sin embargo, es muy razonable preguntarse si no podemos creer que en este resultado vale para los lotes que están en la cuenca del Río Tala. El análisis estadístico realizado no nos permite formular ninguna respuesta a esta pregunta.
El análisis del modelo conceptual, en cambio, produce una respuesta basada en la comparación entre las cuencas de los Ríos Arrecifes y Tala en términos de todas las características (del suelo, del clima, etc.) que se sepa pueden afectar a la descomposición de la materia orgánica. Esta respuesta basada en el modelo conceptual puede, naturalmente, ser correcta o incorrecta. Nosotros no tendremos una medida numérica de cuan seguros podemos estar en esa respuesta. Igualmente, creeremos más o menos según cuan sólido sea el modelo conceptual.