Problema 1
Un
estudio dirigido a mejorar la producción ganadera en el área del pueblo Aconquija (Catamarca) incluyó un experimento para evaluar
técnicas de manejo de la vegetación. Como los pastos de forrajeros que crecen en
el área integran una vegetación dominada por arbustos, se propuso que su
producción podría ser incrementada si se tomaban medidas para eliminar los
arbustos. Por tal razón, se diseñó y condujo un experimento para el cual se
tomaron al azar 18 parcelas de 0,25 has dentro del área de estudio. Cada
parcela fue asignada al azar a uno de los siguientes 3 tratamientos antes del
comienzo de la estación de crecimiento:
(a)
quema
(b)
eliminación mecánica de arbustos
(remoción)
(c)
control sin eliminación de arbustos
Durante la estación de
crecimiento se procedió a medir la la cantidad de
pasto producido (en kg/ha) en cada parcela. A
continuación, se presentan los resultados del análisis de la información
obtenida:
|
|
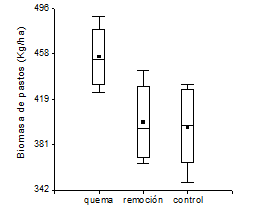
Figura: Distribuciones de
frecuencias observadas de los valores de producción de biomasa de pastos con
tres tratamientos de control de arbustos |
Análisis
de la varianza
Variable
N R² R² Aj
Biomasa pastos 18
0,47 0,40
Cuadro
de Análisis de
F.V. SC gl CM F valor
p
Manejo 13444,11 2 6722,06 6,78
0,0080
Error
14877,67 15 991,84
Total 28321,78 17
(a)
¿Cuales son las unidades
experimentales y cuál es la población de referencia?
(b)
¿Cuántas repeticiones de cada
tratamiento fueron realizadas?
(c)
Interprete la figura presentada en
términos del problema.
(d)
¿Cuál es la hipótesis nula?
(e)
El efecto del fuego sobre la
producción de pastos, ¿se debe a la eliminación de los arbustos?
(f)
Construya intervalos de confianza para
las diferencia de producción esperada de pastos entre los tratamientos.
(g)
Recomiende una práctica de manejo.
Justifique su respuesta.
(h)
Si las 18 parcelas hubieran sido
seleccionadas en tríos en seis localidades
y en cada una de estas localidades se hubieran distribuido al azar los tres
tratamientos. ¿Cuáles hubieran sido las unidades experimentales, cuál la
población de referencia y cuál el diseño?
¿Escribir el modelo que correspondería?
Problema 2
Antes de inscribir sus
nuevas variedades experimentales de trigo, un semillero debe compararlas con un
testigo comercial de buen comportamiento y mostrar que la/s nueva/s variedad/es
es/son superior/es. Para ello se diseña un ensayo de cultivos. Como la fertilidad
del suelo en el lote donde se realiza el experimento es heterogénea, se
establecen 4 bloques. A continuación, se muestran Los datos obtenidos
(rendimiento en qq/ha), así como parte de los
resultados de los análisis estadísticos realizados:
Rendimientos observados
|
|
Variedades de trigo
|
||||
|
Bloques |
Testigo |
Var 1 |
Var 2 |
Var 3 |
Var 4 |
|
I |
24 |
30 |
21 |
28 |
29 |
|
II |
25 |
27 |
22 |
24 |
32 |
|
III |
29 |
27 |
22 |
28 |
33 |
|
IV |
23 |
24 |
20 |
22 |
28 |
Tabla de Análisis de
|
F.V. |
SC |
gl |
CM |
F |
Valor p |
|
Bloques |
50,60 |
|
|
|
|
|
Trats. |
178,30 |
|
|
|
|
|
Error |
34,90 |
|
|
|
|
|
Total |
|
|
|
|
|
Test:Tukey Alfa:=0,05 DMS:=3,84393
Error: 2,9083 gl: 12
|
Tratamiento |
Medias |
n |
|
|
|
|
Var 2 |
21,25 |
4 |
A |
|
|
|
Testigo |
25,25 |
4 |
|
B |
|
|
Var 3 |
25,50 |
4 |
|
B
|
|
|
Var 1 |
27,00 |
4 |
|
B
|
C
|
|
Var 4 |
30,50 |
4 |
|
|
C |
Letras distintas indican
diferencias significativas (p<=0,05)
(a) Proponga un modelo que explique la variación obtenida en los
rendimientos. Explique en significado de cada término.
(b) Plantee la hipótesis nula y alternativa que correspondiente poner a
prueba.
(c) Complete la tabla de análisis de varianza. Someta a prueba la hipótesis
y concluya.
(d) Utilice la prueba de Tukey para identificar
la/s variedad/es que vale la pena introducir al cultivo.
(e) ¿Qué consecuencias tendría para el semillero cometer error de tipo I en
estas pruebas? ¿y error de tipo II?
(f) ¿Que supuestos deben cumplirse para que las conclusiones de este estudio
sean válidas? Póngalos a prueba.
Problema 3
Se realizó un experimento para estudiar los efectos de
la fertilización nitrogenada (sin fertilizante y con fertilizante) y de
profundidad de labranza (0,18 y 0,28m) sobre el rendimiento en azúcar de los
cultivos de remolacha azucarera. Para ello se delimitaron 4 parcelas en 4
sectores de un campo experimental con diferente historia de uso. Dentro de cada
sector se asignó a cada parcela un tratamiento combinado de fertilización y
labranza elegido al azar. En todas las parcelas se cultivó remolacha azucarera
y se midió el rendimiento en kg de azucar/parcela. A continuación se presentan los datos
obtenidos y los resultados el análisis de la varianza realizado con ellos:
Rendimiento
en azucar [kg/parcela]
|
Bloque |
N0 |
N1 |
||
|
0,18m |
0,28m |
0,18m |
0,28m |
|
I
|
4,59 |
4,75 |
5,36 |
5,63 |
|
II |
4,65 |
4,80 |
6,00 |
6,20 |
|
III |
5,00 |
5,20 |
6,35 |
6,80 |
|
IV |
5,50 |
5,80 |
6,78 |
7,25 |
Tabla de Análisis de la Varianza
Fuente de Variación SC
GL CM F p-valor
PROFUNDIDAD (B) 0,30 1 0,30 9,28 0,0139
NITRÓGENO(A) 6,35 1 6,35 194,81 <0,0001
BLOQUES 3,51 3 1,17 35,93 <0,0001
PROF (B)*NITRÓG(A)
0,02 1 0,02 0,64
0,4426
Error 0,29 9 0,03
Total 10,48 15
(a) ¿Qué diseño experimental fue utilizado? Proponer un diagrama del
posible trazado de las parcelas en el campo.
(b) Escriba el modelo y describa los parámetros en términos del problema.
(c) Pruebe las hipótesis de interés a un nivel de significación del 5%.
(d) Estime el efecto principal del nivel 0 de N y el efecto simple o
específico del mismo nivel de nitrógeno cuando la profundidad de labranza es de
0,28m.
(e) ¿Qué tratamiento recomienda?
Problema 4
En los últimos
años se ha difundido en el noroeste argentino la práctica de sembrar maíz con
distancias entre surcos de
|
Rendimientos [kg/ha] |
||||
|
Distancia entre surcos [cm] |
Bloque |
Híbrido |
||
|
´8480 |
2A120 |
DK834MG |
||
|
52 |
1 |
6300 |
7250 |
6645 |
|
2 |
9501 |
9500 |
10108 |
|
|
3 |
8263,8 |
9350 |
9690 |
|
|
4 |
5831 |
6800 |
6341,4 |
|
|
70 |
1 |
8320 |
10105 |
8913 |
|
2 |
10800 |
13342 |
12170 |
|
|
3 |
9800 |
12000 |
13700 |
|
|
4 |
8980 |
9200 |
8304 |
|
(a) Proponga un posible diagrama
de campo indicando la asignación de los tratamientos a las unidades
experimentales.
(b) Plantee el modelo
estadístico apropiado para comparar los efectos combinados de las dos distancias
entre surcos y de las diferencias entre los tres cultivares de maíz incluidos
en el ensayo sobre el rendimiento esperado. Explique el significado de cada
parte del modelo en términos del problema (distinguir efectos principales de
interacción).
(c) Construya un gráfico que
permita apreciar si los efectos de la distancia entre surcos sobre el
rendimiento de los cultivos parecen variar entre diferentes cultivares
híbridos.
(d) Estime los efectos simples
de las distancias entre surcos para el Híbrido 2A120 y compárelos con las
estimaciones de los efectos simples de las distancias entre surcos para el
Híbrido DK834MG.
(e) Construya la tabla de
análisis de la varianza y ponga a prueba las hipótesis necesarias para evaluar
y caracterizar los efectos de los factores manipulados en el experimento.
(f) ¿Qué híbrido y a que
distancia entre surcos recomendaría para la zona?
(g) Poner a prueba los supuestos
de distribución normal de los errores y de homogeneidad de varianzas
Problema 5
Para estudiar el
efecto de la fertilización nitrogenada y del riego sobre el rendimiento de
maíz, se propuso el siguiente modelo:
![]() con
con ![]() ~
N(0,σ2)i.i.d
~
N(0,σ2)i.i.d
Donde
yi= rendimiento de maíz en la
parcela i-ésima
![]() xi= nivel de fertilización
nitrogenada de la parcela i-ésima en kg/ha
xi= nivel de fertilización
nitrogenada de la parcela i-ésima en kg/ha
zi= 0 si la parcela no recibió riego
1 si la parcela recibió riego
(a) Plantee las hipótesis de
interés para evaluar el efecto del riego.
(b) Indique cuál de las
hipótesis se rechazaría en cada una de las situaciones descriptas por los
siguientes gráficos.
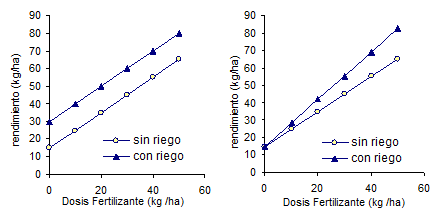
(c) ¿Cuál es el signo que
esperaría para los coeficientes β2 y β3 en cada
caso?
(d) Interprete los resultados
que presentan los gráficos en términos del problema.
Problema
6
Un
ingeniero agrónomo supone que el tamaño del invernáculo y la temperatura media
mensual inciden sobre el gasto de energía eléctrica mensual del invernáculo.
Para poner a prueba esta suposición registró la siguiente información en
distintos invernáculos, y realizo un análisis de regresión múltiple. A
continuación se muestran los datos y parte de los resultados del análisis
|
Invernáculo |
gasto mensual de energía
eléctrica (kW) |
tamaño del invernáculo
(m2) |
T (ºC) |
|
1 |
2260 |
3000 |
21,1 |
|
2 |
2420 |
3200 |
22,2 |
|
3 |
2420 |
3220 |
26,6 |
|
4 |
2710 |
3600 |
29,4 |
|
5 |
2740 |
3640 |
30,0 |
|
6 |
2800 |
3700 |
27,2 |
|
7 |
2830 |
3710 |
23,3 |
|
8 |
2900 |
3800 |
21,6 |
|
9 |
2990 |
3900 |
20,0 |
|
10 |
3240 |
4200 |
16,7 |
Coef Est. EE
const -60,56 14,15
T (ºC) -3,86 0,26
tamaño del invernaculo 0,80 3,1E-03
SCTotal = 785090 SCError = 71.38
(a) Interprete los coeficientes
de regresión estimados en términos del problema. Especifique las unidades
correspondientes.
(b) Construya la tabla de ANOVA
Ponga a prueba la hipótesis global que dice que los coeficientes de regresión
parcial son iguales a ceco (nivel de significación
del 5%)
(c) ¿Son ambas variables útiles
para predecir el gasto esperado de energía eléctrica en el invernáculo? Ponga a prueba las hipótesis que considere
necesarias para responder a esta pregunta.
(d) Calcule e interprete el
coeficiente de determinación.
(e) Calcule el residual de la
segunda observación.
(f) ¿Qué supuestos deberían
cumplirse para la estimación de los parámetros y las pruebas posteriores en el
análisis de regresión? Ponga a prueba los supuestos.
Problema
7
Se estudiaron
los efectos de tres frecuencias de corte y de tres alturas de corte sobre la
producción de materia seca de una pastura tropical. Como el sitio experimental
presenta heterogeneidad de suelos, se dividió en cuatro bloques. Se presentan
los datos obtenidos (kg/parcela) junto con resultados
parciales del análisis de la varianza:
|
frecuencia de corte |
altura de corte |
bloque1 |
bloque2 |
bloque3 |
bloque4 |
|
20 |
Baja |
5,69 |
5,98 |
5,37 |
6,3 |
|
Media |
3,72 |
3,2 |
3,9 |
4,51 |
|
|
Alta |
3,66 |
2,85 |
2,6 |
3,83 |
|
|
40 |
Baja |
6,48 |
7,92 |
4,74 |
6,3 |
|
Media |
3,86 |
4,54 |
4,42 |
5,06 |
|
|
Alta |
11,15 |
3,54 |
3,91 |
3,66 |
|
|
60 |
Baja |
4,9 |
5,73 |
12 |
8,56 |
|
Media |
5,34 |
4,28 |
6,16 |
6,34 |
|
|
Alta |
3,4 |
5,47 |
4,78 |
3,75 |
|
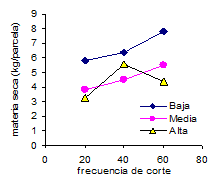
Tabla y grafico de
promedios
Promedio gral.= 5.22 SCTotal= 149.5 SCBloque= 1.79 SCFrecuencia= 16.29 SCAltura= 37.88 |
|
|||||||||||||||||||
(a) Construya un diagrama de
campo con una posible asignación de los tratamientos.
(b) Identifique factores y
tratamientos. Clasifique los factores. Postule un modelo estadístico que de
cuenta de los efectos de la frecuencia y de la altura de corte sobre la producción
de pasto en el sistema estudiado.
(c) Plantee las hipótesis de
interés y póngalas a prueba con un nivel de significación del 5%. Compare el
resultado de las pruebas de hipótesis con el grafico presentado.
(d) Utilice la prueba de Tukey para identificar el tratamiento de la pastura que
corresponde recomendar para obtener el mayor
producción de pasto esperada.
Problema
8
Las
plantas superiores requieren estar hidratadas para mantener su capacidad de
captar CO2 del aire para la fotosíntesis. Esto se debe a que el CO2
entra a sus hojas sólo por poros (llamados estomas) que únicamente están
abiertos cuando las hojas están hidratadas. Las plantas inferiores, que no
tienen estomas, tienen a veces respuestas más complicadas que esta a las
condiciones de humedad. Por ejemplo, se ha visto que el liquen Ramalina maciformis
aumenta su tasa de fotosíntesis cuando pasa de estar seco a estar húmedo pero
que pasado un límite de humedad disminuye la tasa de fotosíntesis porque el CO2
difunde más lentamente en medio acuoso que en medio gaseoso. En un estudio
dirigido a evaluar si el musgo Barbula aurea presenta una respuesta parecida se tomaron 10
talos de este musgo de peso similar, se los sometió a diferentes grados de
hidratación asignados al azar y se midió su tasa de fotosíntesis. Los datos
obtenidos son los siguientes:
|
Unidad experimental (talo) |
Hidratación [g agua/g materia seca] |
Fotosíntesis [mg
CO2/g materia seca. hora] |
|
1 |
1,0 |
13,4 |
|
2 |
1,4 |
16,9 |
|
3 |
1,8 |
19,2 |
|
4 |
2,2 |
17,2 |
|
5 |
2,6 |
18,6 |
|
6 |
3,0 |
17,2 |
|
7 |
3,2 |
14,8 |
|
8 |
3,4 |
16,1 |
|
9 |
3,8 |
11,4 |
|
10 |
4,0 |
12,0 |
(a) Construir e interpretar un
gráfico de dispersión que permita apreciar la relación estadística entre la tasa
de fotosíntesis y el grado de hidratación de este musgo.
(b) Formular un modelo de
regresión apropiado para examinar la asociación entre la tasa esperada de
fotosíntesis y el grado de hidratación de este musgo.
(c) Explicar el significado y
especificar sus unidades de cada uno de los parámetros del modelo.
(d) Estimar los parámetros del
modelo y poner a prueba la hipótesis nula que dice que el efecto de las
diferencias en hidratación del musgo sobre su tasa esperada de fotosíntesis
varía con nivel de hidratación.
(e) Señalar los supuestos del
análisis.
(f) Concluir en términos del
problema.